Funciones polinomiales:
Las funciones polinomiales están entre las expresiones mas sencillas del álgebra. Es fácil evaluarlas, solo requieren sumas multiplicaciones repetidas. Debido a esto, con frecuencia se usan para aproximar otras funciones mas complicadas. Una función polinomial es una función cuya regla esta dada por un polinomio en una variable. El grado de una función polinomial es el grado del polinomio en una variable, es decir, la potencia mas alta que aparece de x.
Función algebraica
En matemáticas, una función algebraica es una función que satisface una ecuación polinómica cuyos coeficientes son a su vez polinomios o monomios. Por ejemplo, una función algebraica de una variable x es una solución y a la ecuación
donde los coeficientes ai(x) son funciones polinómicas de x. Una función que no es algebraica es denominada una función trascendente.
En términos más precisos, una función algebraica puede no ser estrictamente una función, por lo menos no en el sentido convencional. Por ejemplo sea la ecuación de una circunferencia:
La misma determina y, excepto por su signo:
Sin embargo, se considera que ambas ramas pertenecen a la "función" determinada por la ecuación polinómica.
Una función algebraica de n variables es definida en forma similar a la función y que es solución de la ecuación polinómica en n + 1 variables:
Normalmente se supone que p debe ser un polinomio irreducible. La existencia de una función algebraica es asegurada por el teorema de la función implícita.
Formalmente, una función algebraica de n variables en el cuerpo K es un elemento del cierre algebraico del cuerpo de las funciones racionales K(x1,...,xn). Para poder comprender a las funciones algebraicas como funciones, es necesario incorporar ideas relativas a las superficies de Riemann o en un ámbito más general sobre variedades algebraicas, y teoría de haces.
Función trascendente
Una función trascendente es una función que no satisface una ecuación polinomial cuyos coeficientes sean a su vez polinomios; esto contrasta con las funciones algebraicas, las cuales satisfacen dicha ecuación. En otras palabras, una función trascendente es una función que trasciende al álgebra en el sentido que no puede ser expresada en términos de una secuencia finita de operaciones algebraicas de suma, resta y extracción de raíces. Una función de una variable es trascendente si es independiente en un sentido algebraico de dicha variable.
Raíz de una función
En matemática, se conoce como raíz (o cero) de una función (definida sobre un cierto cuerpo algebraico) f(x) a todo elemento xperteneciente al dominio de dicha función tal que se cumpla:
.
Por ejemplo, dada la función:
Planteando y resolviendo la ecuación:
Se tiene que 2 y 4 son raíces ya que f(2) = 0 y f(4) = 0.
Buscando raíces
- El teorema fundamental del álgebra determina que todo polinomio en una variable compleja y de grado n tiene n raíces (contando sus multiplicidades). Aun así, Las raíces de los polinomios reales no son necesariamente reales; algunas de ellas, o incluso todas, pueden ser complejas.
- Una función trascendente como por ejemplo
 posee una infinidad de raíces, concretamente cualquier
posee una infinidad de raíces, concretamente cualquier  es raíz de esa función. En cambio la función
es raíz de esa función. En cambio la función  no se anula nunca sobre los números complejos.
no se anula nunca sobre los números complejos. - El número de raíces de una función holomorfa o una función analítica es un conjunto numerable sin puntos de acumulación.
- Uno de los problemas no resueltos más interesantes de la matemática moderna es encontrar las raíces de la función zeta de Riemann.
Teorema fundamental del álgebra
El teorema fundamental del álgebra establece que un polinomio en una variable, no constante y con coeficientes complejos, tiene tantas raíces como indica su grado, contando las raíces con sus multiplicidades. En otras palabras, dado un polinomio complejo  de grado
de grado  , la ecuación
, la ecuación  tiene exactamente
tiene exactamente 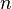 soluciones complejas, contando multiplicidades. De manera equivalente:
soluciones complejas, contando multiplicidades. De manera equivalente:
 de grado
de grado  , la ecuación
, la ecuación  tiene exactamente
tiene exactamente 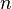 soluciones complejas, contando multiplicidades. De manera equivalente:
soluciones complejas, contando multiplicidades. De manera equivalente:- El cuerpo de los complejos es cerrado para las operaciones algebraicas.
- Todo polinomio complejo de grado n se puede expresar como un producto de n polinomios de la forma
 .
.
El teorema se establece comúnmente de la siguiente manera:
|
Aunque ésta en principio parece ser una declaración más débil, implica fácilmente la forma completa por la división polinómica sucesiva por factores lineales.
El nombre del teorema es considerado ahora un error por muchos matemáticos, puesto que es más un teorema del análisis matemático que del álgebra.
Corolarios
Como el teorema fundamental del álgebra puede ser visto como la declaración de que el cuerpo de los números complejos es algebraicamente cerrado, se sigue que cualquier teorema concerniente a cuerpos algebraicamente cerrados aplican al cuerpo de los números complejos. Se muestran aquí algunas consecuencias del teorema, acerca del cuerpo de los números reales o acerca de las relaciones entre el cuerpo de los reales y el cuerpo de los complejos:
- El cuerpo de los números complejos es la clausura algebraica del cuerpo de números reales.
- Todo polinomio en una variable
 con coeficientes reales es el producto de un polinomio constante de la forma
con coeficientes reales es el producto de un polinomio constante de la forma  con
con  real, y polinomios de la forma
real, y polinomios de la forma  con
con  y
y  reales y
reales y  (que es lo mismo que decir que el polinomio
(que es lo mismo que decir que el polinomio  no tiene raíces reales).
no tiene raíces reales).
- Toda función racional en una variable
 , con coeficientes reales, se puede escribir como la suma de una función polinómica con funciones racionales de la forma
, con coeficientes reales, se puede escribir como la suma de una función polinómica con funciones racionales de la forma  (donde
(donde 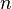 es un número natural, y
es un número natural, y  y
y  son números reales), y funciones racionales de la forma
son números reales), y funciones racionales de la forma  (donde
(donde 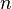 es un número natural, y
es un número natural, y  ,
,  ,
,  , y
, y  son números reales tales que
son números reales tales que  ). Un corolario de esto es que toda función racional en una variable y coeficientes reales tiene una primitiva elemental.
). Un corolario de esto es que toda función racional en una variable y coeficientes reales tiene una primitiva elemental.
- Toda extensión algebraica del cuerpo de los reales es isomorfa al cuerpo de los reales o al cuerpo de los complejos.







No hay comentarios:
Publicar un comentario